| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 3 (Before Exercise 3.1) | Exercise 3.1 | Example 4 to 7 (Before Exercise 3.2) |
| Exercise 3.2 | Example 8 to 10 (Before Exercise 3.3) | Exercise 3.3 |
Chapter 3 Data Handling
Welcome to the solutions guide for Chapter 3, "Data Handling," meticulously aligned with the latest Class 7 NCERT mathematics textbook for the academic session 2024-25. This chapter significantly expands upon earlier introductions to data, equipping students with essential tools for organizing, visually representing, and analyzing information drawn from the world around them. A key development at this stage is the introduction to measures that summarize data sets and the fundamental concepts of chance and probability. These solutions provide comprehensive, step-by-step methods to navigate the exercises effectively, ensuring a robust understanding of these crucial statistical concepts.
The journey through data handling begins with managing raw information. The solutions demonstrate systematic techniques for collecting and organizing data, often employing tools like frequency distribution tables to bring structure to unordered observations. Building on this organization, the chapter introduces crucial measures of central tendency – single values that attempt to describe the center of a data set. The solutions provide detailed calculations and conceptual clarity for:
- The Arithmetic Mean (Average): Calculated as $\text{Mean} = \frac{\sum \limits_{i=1}^{n} x_i}{n}$, or more simply, $\frac{\text{Sum of all observations}}{\text{Number of observations}}$.
- The Median: The middle value of a data set when arranged in ascending or descending order. The solutions explain how to find the median for both odd and even numbers of observations.
- The Mode: The value that appears most frequently in the data set. A dataset can have one mode, more than one mode, or no mode.
Effective communication of data often relies on visual representation. This chapter places significant emphasis on bar graphs. The solutions provide meticulous guidance on constructing accurate and informative graphs:
- Single Bar Graphs: Representing data using bars of uniform width, where the height corresponds to the frequency or value.
- Double Bar Graphs: A powerful tool for comparing two related data sets side-by-side for different categories.
A significant addition in Class 7 is the introduction to Chance and Probability. The solutions gently introduce the concepts of likelihood and randomness. They explain how to calculate the probability of simple events, defining probability as the ratio measuring the likelihood of an occurrence: $P(\text{Event}) = \frac{\text{Number of outcomes favourable to the event}}{\text{Total number of possible outcomes}}$ Solved examples typically involve everyday scenarios like tossing a fair coin (probability of heads, $P(H) = \frac{1}{2}$), rolling a standard six-sided die (e.g., probability of getting an even number, $P(\text{Even}) = \frac{3}{6} = \frac{1}{2}$), or selecting an object from a known collection.
Regarding the rationalized syllabus for 2024-25, Chapter 3, "Data Handling," in the Class 7 NCERT textbook has retained its core focus on Mean, Median, Mode, Bar Graphs (including Double Bar Graphs), and the introduction to Probability. The rationalization primarily involved adjustments to the volume and complexity of exercises, ensuring students develop a strong foundational understanding of these key statistical concepts without excessive repetition or delving into overly complex data scenarios. By engaging with these comprehensive solutions, students can master systematic data handling techniques, confidently calculate and interpret central tendencies, become proficient in creating and reading bar graphs for effective data visualization and comparison, and gain a solid initial grasp of probability.
Example 1 to 3 (Before Exercise 3.1)
Example 1. Ashish studies for 4 hours, 5 hours and 3 hours respectively on three consecutive days. How many hours does he study daily on an average?
Answer:
Given:
Study hours on three consecutive days are 4 hours, 5 hours, and 3 hours.
To Find:
The average daily study hours.
Solution:
The average is calculated by dividing the total sum of quantities by the number of quantities.
In this case, the quantities are the study hours on each day, and the number of quantities is the number of days.
Total study hours = Study hours on Day 1 + Study hours on Day 2 + Study hours on Day 3
Total study hours = $4 + 5 + 3$ hours
Total study hours = $12$ hours
Number of days = $3$
Average study hours = $\frac{\text{Total study hours}}{\text{Number of days}}$
Average study hours = $\frac{12}{3}$ hours
Average study hours = $4$ hours
So, Ashish studies for $4$ hours daily on an average.
Example 2. A batsman scored the following number of runs in six innings:
| 36 | 35 | 50 | 46 | 60 | 55 |
Calculate the mean runs scored by him in an inning.
Answer:
Given:
The runs scored by a batsman in six innings are $36, 35, 50, 46, 60, 55$.
To Find:
The mean runs scored by the batsman in an inning.
Solution:
The mean (or average) of a set of observations is calculated by dividing the sum of all observations by the total number of observations.
The given observations (runs scored) are: $36, 35, 50, 46, 60, 55$.
Total number of innings (observations) = $6$
Sum of runs scored in all innings = $36 + 35 + 50 + 46 + 60 + 55$
Sum of runs = $282$
The formula for the mean is:
Mean = $\frac{\text{Sum of observations}}{\text{Number of observations}}$
Substitute the values into the formula:
Mean runs = $\frac{282}{6}$
Now, perform the division:
Mean runs = $47$
Therefore, the mean runs scored by the batsman in an inning is $47$.
Example 3. The ages in years of 10 teachers of a school are:
| 32 | 41 | 28 | 54 | 35 | 26 | 23 | 33 | 38 | 40 |
(i) What is the age of the oldest teacher and that of the youngest teacher?
(ii) What is the range of the ages of the teachers?
(iii) What is the mean age of these teachers?
Answer:
Given:
The ages in years of 10 teachers of a school are: 32, 41, 28, 54, 35, 26, 23, 33, 38, 40.
To Find:
(i) The age of the oldest teacher and that of the youngest teacher.
(ii) The range of the ages of the teachers.
(iii) The mean age of these teachers.
Solution:
The given ages of the 10 teachers are:
32, 41, 28, 54, 35, 26, 23, 33, 38, 40.
To easily find the minimum and maximum ages, let's arrange the ages in ascending order:
23, 26, 28, 32, 33, 35, 38, 40, 41, 54.
Now, we can answer each part of the question.
(i) Age of the oldest teacher and the youngest teacher:
From the sorted list, the lowest age is $23$ years and the highest age is $54$ years.
The age of the youngest teacher is $23$ years.
The age of the oldest teacher is $54$ years.
(ii) Range of the ages:
The range of a set of data is the difference between the highest and the lowest values in the data set.
Range = Highest age - Lowest age
Range = $54 - 23$
Range = $31$ years
The range of the ages of the teachers is $31$ years.
(iii) Mean age:
The mean of a set of observations is calculated by dividing the sum of all observations by the total number of observations.
Number of teachers (observations) = $10$
Sum of ages = $32 + 41 + 28 + 54 + 35 + 26 + 23 + 33 + 38 + 40$
Sum of ages = $350$
Mean age = $\frac{\text{Sum of ages}}{\text{Number of teachers}}$
Mean age = $\frac{350}{10}$
Mean age = $35$ years
The mean age of these teachers is $35$ years.
Exercise 3.1
Question 1. Find the range of heights of any ten students of your class
Answer:
Given:
Heights of any ten students of a class (data needs to be collected).
To Find:
The range of the heights of these ten students.
Solution:
To find the range of heights of ten students in your class, you would first need to measure the height of each of those ten students.
Let's assume, for the purpose of demonstration, that the heights (in centimeters) of ten students are:
150, 155, 160, 148, 165, 152, 158, 163, 151, 157.
To find the range, we first need to identify the minimum and maximum values from this set of data.
Arranging the hypothetical heights in ascending order makes it easier to find the minimum and maximum values:
148, 150, 151, 152, 155, 157, 158, 160, 163, 165.
The lowest height in this set is $148$ cm.
The highest height in this set is $165$ cm.
Now, we calculate the range using the formula:
Range = Highest Value - Lowest Value
Using the hypothetical data:
Range = $165$ cm - $148$ cm
Range = $17$ cm
So, for this hypothetical data, the range of heights is $17$ cm.
To find the actual range for ten students in your class, you would follow these steps:
1. Measure the height of each of the ten students.
2. List the ten heights you measured.
3. Identify the lowest height (minimum value) from your list.
4. Identify the highest height (maximum value) from your list.
5. Calculate the difference between the highest height and the lowest height. This difference is the range of heights for those ten students.
Question 2. Organise the following marks in a class assessment, in a tabular form.
| 4 | 6 | 7 | 5 | 3 | 5 | 4 | 5 | 2 | 6 |
| 2 | 5 | 1 | 9 | 6 | 5 | 8 | 4 | 6 | 7 |
(i) Which number is the highest?
(ii) Which number is the lowest?
(iii) What is the range of the data?
(iv) Find the arithmetic mean.
Answer:
Given:
The marks in a class assessment are: 4, 6, 7, 5, 3, 5, 4, 5, 2, 6, 2, 5, 1, 9, 6, 5, 8, 4, 6, 7.
To Organize and Find:
Organise the marks in a tabular form (frequency distribution).
(i) Which number is the highest?
(ii) Which number is the lowest?
(iii) What is the range of the data?
(iv) Find the arithmetic mean.
Solution:
First, let's organize the given marks in a tabular form showing the frequency of each mark.
The marks are: 4, 6, 7, 5, 3, 5, 4, 5, 2, 6, 2, 5, 1, 9, 6, 5, 8, 4, 6, 7.
Let's count the frequency of each mark (from 1 to 9):
Mark 1: Appears 1 time
Mark 2: Appears 2 times
Mark 3: Appears 1 time
Mark 4: Appears 3 times
Mark 5: Appears 5 times
Mark 6: Appears 4 times
Mark 7: Appears 2 times
Mark 8: Appears 1 time
Mark 9: Appears 1 time
Total number of marks = $1 + 2 + 1 + 3 + 5 + 4 + 2 + 1 + 1 = 20$. There are 20 marks in total.
Here is the data organized in a tabular form (Frequency Distribution Table):
| Mark | Tally Marks | Frequency |
| 1 | $|$ | 1 |
| 2 | $||$ | 2 |
| 3 | $|$ | 1 |
| 4 | $|||$ | 3 |
| 5 | $\bcancel{||||}$ | 5 |
| 6 | $||||$ | 4 |
| 7 | $||$ | 2 |
| 8 | $|$ | 1 |
| 9 | $|$ | 1 |
Now, let's answer the questions.
(i) Which number is the highest?
Looking at the list of marks (1, 2, 3, 4, 5, 6, 7, 8, 9) and their frequencies, the highest mark obtained by any student is 9.
The highest number is 9.
(ii) Which number is the lowest?
Looking at the list of marks (1, 2, 3, 4, 5, 6, 7, 8, 9) and their frequencies, the lowest mark obtained by any student is 1.
The lowest number is 1.
(iii) What is the range of the data?
The range is the difference between the highest and lowest values in the data set.
Range = Highest Mark - Lowest Mark
Range = $9 - 1$
Range = $8$
The range of the data is 8.
(iv) Find the arithmetic mean.
The arithmetic mean is calculated by dividing the sum of all observations by the total number of observations.
Sum of all marks = $(1 \times 1) + (2 \times 2) + (3 \times 1) + (4 \times 3) + (5 \times 5) + (6 \times 4) + (7 \times 2) + (8 \times 1) + (9 \times 1)$
Sum of marks = $1 + 4 + 3 + 12 + 25 + 24 + 14 + 8 + 9$
Sum of marks = $100$
Total number of observations (marks) = $20$
Mean = $\frac{\text{Sum of marks}}{\text{Total number of marks}}$
Mean = $\frac{100}{20}$
Mean = $5$
The arithmetic mean of the marks is 5.
Question 3. Find the mean of the first five whole numbers.
Answer:
Given:
The first five whole numbers.
To Find:
The mean of the first five whole numbers.
Solution:
The whole numbers start from 0 and continue indefinitely (0, 1, 2, 3, ...).
The first five whole numbers are 0, 1, 2, 3, and 4.
To find the mean of these numbers, we use the formula:
Mean = $\frac{\text{Sum of observations}}{\text{Number of observations}}$
Sum of the first five whole numbers = $0 + 1 + 2 + 3 + 4$
Sum = $10$
Number of observations = $5$ (since there are five numbers)
Now, substitute the values into the formula:
Mean = $\frac{10}{5}$
Mean = $2$
Therefore, the mean of the first five whole numbers is 2.
Question 4. A cricketer scores the following runs in eight innings:
| 58 | 76 | 40 | 35 | 46 | 45 | 0 | 100 |
Find the mean score.
Answer:
Given:
The runs scored by a cricketer in eight innings are: 58, 76, 40, 35, 46, 45, 0, 100.
Number of innings = 8.
To Find:
The mean score.
Solution:
The mean score is calculated by dividing the total runs scored by the number of innings played.
The given runs in eight innings are:
58, 76, 40, 35, 46, 45, 0, 100.
Total number of innings = 8.
Sum of runs scored in all innings = $58 + 76 + 40 + 35 + 46 + 45 + 0 + 100$
Sum of runs = $400$
The formula for the mean is:
Mean score = $\frac{\text{Sum of runs}}{\text{Number of innings}}$
Substitute the values into the formula:
Mean score = $\frac{400}{8}$
Perform the division:
Mean score = $50$
Therefore, the mean score of the cricketer is 50 runs.
Question 5. Following table shows the points of each player scored in four games:
| Player | Game 1 | Game 2 | Game 3 | Game 4 |
|---|---|---|---|---|
| A | 14 | 16 | 10 | 10 |
| B | 0 | 8 | 6 | 4 |
| C | 8 | 11 | Did not Play | 13 |
Now answer the following questions:
(i) Find the mean to determine A’s average number of points scored per game.
(ii) To find the mean number of points per game for C, would you divide the total points by 3 or by 4? Why?
(iii) B played in all the four games. How would you find the mean?
(iv) Who is the best performer?
Answer:
(i) Find the mean to determine A’s average number of points scored per game.
To find the mean (average) number of points scored per game for Player A, we sum the points scored by A in all the games A played and divide by the number of games A played.
Player A's scores in the four games are: 14, 16, 10, 10.
Number of games played by A = 4
Sum of A's scores = $14 + 16 + 10 + 10 = 50$
Mean score for A = $\frac{\text{Sum of A's scores}}{\text{Number of games played by A}}$
Mean score for A = $\frac{50}{4}$
Mean score for A = $12.5$
The mean number of points scored per game by Player A is 12.5.
(ii) To find the mean number of points per game for C, would you divide the total points by 3 or by 4? Why?
To find the mean number of points per game for Player C, you would divide the total points by 3.
This is because the mean (average) is calculated by dividing the sum of observations by the number of observations. Player C participated and scored points in only 3 games. Game 3 is marked as "Did not Play", which means it is not included in the data points for calculating the average performance per game based on actual play.
(iii) B played in all the four games. How would you find the mean?
To find the mean number of points per game for Player B, who played in all four games, we sum the points scored by B in all four games and divide by the total number of games B played, which is 4.
Player B's scores in the four games are: 0, 8, 6, 4.
Number of games played by B = 4
Sum of B's scores = $0 + 8 + 6 + 4 = 18$
Mean score for B = $\frac{\text{Sum of B's scores}}{\text{Number of games played by B}}$
Mean score for B = $\frac{18}{4}$
Mean score for B = $4.5$
(iv) Who is the best performer?
To determine the best performer based on the average points per game, we compare the mean scores of all three players (A, B, and C).
From part (i), Mean score for A = 12.5
From part (iii), Mean score for B = 4.5
Now, we calculate the mean score for Player C.
Player C's scores in the games played are: 8 (Game 1), 11 (Game 2), 13 (Game 4).
Number of games played by C = 3
Sum of C's scores = $8 + 11 + 13 = 32$
Mean score for C = $\frac{\text{Sum of C's scores}}{\text{Number of games played by C}}$
Mean score for C = $\frac{32}{3} \approx 10.67$
Comparing the mean scores of the three players:
- Mean score for A = 12.5
- Mean score for B = 4.5
- Mean score for C $\approx$ 10.67
The highest mean score is 12.5, which belongs to Player A.
Therefore, based on the average number of points scored per game, Player A is the best performer.
Question 6. The marks (out of 100) obtained by a group of students in a science test are 85, 76, 90, 85, 39, 48, 56, 95, 81 and 75. Find the:
(i) Highest and the lowest marks obtained by the students.
(ii) Range of the marks obtained.
(iii) Mean marks obtained by the group.
Answer:
Given marks obtained by a group of students in a science test are: 85, 76, 90, 85, 39, 48, 56, 95, 81, and 75.
(i) Highest and the lowest marks obtained by the students.
Let's arrange the marks in ascending order to easily identify the highest and lowest marks:
39, 48, 56, 75, 76, 81, 85, 85, 90, 95
The highest mark obtained by the students is the largest value in the list, which is 95.
The lowest mark obtained by the students is the smallest value in the list, which is 39.
(ii) Range of the marks obtained.
The range is the difference between the highest and the lowest values in the data set.
Range = Highest mark - Lowest mark
Range = $95 - 39$
Range = $56$
The range of the marks obtained is 56.
(iii) Mean marks obtained by the group.
The mean is calculated by summing all the observations and dividing by the total number of observations.
Sum of marks = $85 + 76 + 90 + 85 + 39 + 48 + 56 + 95 + 81 + 75$
Sum of marks = $730$
Number of students (observations) = 10
Mean marks = $\frac{\text{Sum of marks}}{\text{Number of students}}$
Mean marks = $\frac{730}{10}$
Mean marks = $73$
The mean marks obtained by the group is 73.
Question 7. The enrolment in a school during six consecutive years was as follows:
| 1555 | 1670 | 1750 | 2013 | 2540 | 2820 |
Find the mean enrolment of the school for this period.
Answer:
The enrolment in the school during six consecutive years is given as:
1555, 1670, 1750, 2013, 2540, 2820.
To find the mean enrolment, we need to sum the enrolments for all six years and divide by the number of years (which is 6).
Sum of enrolments = $1555 + 1670 + 1750 + 2013 + 2540 + 2820$
Sum of enrolments = $12348$
Number of years = 6
Mean enrolment = $\frac{\text{Sum of enrolments}}{\text{Number of years}}$
Mean enrolment = $\frac{12348}{6}$
Mean enrolment = $2058$
The mean enrolment of the school for this period is 2058.
Question 8. The rainfall (in mm) in a city on 7 days of a certain week was recorded as follows:
| Days | Mon | Tue | Wed | Thurs | Fri | Sat | Sun |
|---|---|---|---|---|---|---|---|
| Rainfall (in mm) | 0.0 | 12.2 | 2.1 | 0.0 | 20.5 | 5.5 | 1.0 |
(i) Find the range of the rainfall in the above data.
(ii) Find the mean rainfall for the week.
(iii) On how many days was the rainfall less than the mean rainfall.
Answer:
The rainfall (in mm) in a city on 7 days of a certain week was recorded as follows: 0.0, 12.2, 2.1, 0.0, 20.5, 5.5, 1.0.
(i) Find the range of the rainfall in the above data.
The given rainfall data points are: 0.0, 12.2, 2.1, 0.0, 20.5, 5.5, 1.0.
To find the range, we need to identify the highest and lowest values in the data set.
Highest rainfall = $20.5$ mm (on Friday)
Lowest rainfall = $0.0$ mm (on Monday and Thursday)
Range = Highest rainfall - Lowest rainfall
Range = $20.5 - 0.0$
Range = $20.5$ mm
The range of the rainfall in the above data is 20.5 mm.
(ii) Find the mean rainfall for the week.
To find the mean rainfall, we sum the rainfall amounts for all 7 days and divide by the number of days.
Sum of rainfall = $0.0 + 12.2 + 2.1 + 0.0 + 20.5 + 5.5 + 1.0$
Sum of rainfall = $41.3$ mm
Number of days = 7
Mean rainfall = $\frac{\text{Sum of rainfall}}{\text{Number of days}}$
Mean rainfall = $\frac{41.3}{7}$
Now, we perform the division:
Mean rainfall $\approx 5.9$ mm (approximately)
The mean rainfall for the week is approximately 5.9 mm.
(iii) On how many days was the rainfall less than the mean rainfall.
The mean rainfall is $\frac{41.3}{7} \approx 5.9$ mm.
We compare each day's rainfall with the mean rainfall (approximately 5.9 mm):
- Monday: 0.0 mm ($0.0 < 5.9$)
- Tuesday: 12.2 mm ($12.2 > 5.9$)
- Wednesday: 2.1 mm ($2.1 < 5.9$)
- Thursday: 0.0 mm ($0.0 < 5.9$)
- Friday: 20.5 mm ($20.5 > 5.9$)
- Saturday: 5.5 mm ($5.5 < 5.9$)
- Sunday: 1.0 mm ($1.0 < 5.9$)
The days when the rainfall was less than the mean rainfall are Monday, Wednesday, Thursday, Saturday, and Sunday.
Counting these days, there are 5 days.
On 5 days, the rainfall was less than the mean rainfall.
Question 9. The heights of 10 girls were measured in cm and the results are as follows:
| 135 | 150 | 139 | 128 | 151 | 132 | 146 | 149 | 143 | 141 |
(i) What is the height of the tallest girl?
(ii) What is the height of the shortest girl?
(iii) What is the range of the data?
(iv) What is the mean height of the girls?
(v) How many girls have heights more than the mean height.
Answer:
Given heights of 10 girls in cm are: 135, 150, 139, 128, 151, 132, 146, 149, 143, 141.
(i) What is the height of the tallest girl?
To find the height of the tallest girl, we need to find the maximum value in the given set of heights.
The given heights are: 135, 150, 139, 128, 151, 132, 146, 149, 143, 141.
Comparing the values, the highest height is 151 cm.
The height of the tallest girl is 151 cm.
(ii) What is the height of the shortest girl?
To find the height of the shortest girl, we need to find the minimum value in the given set of heights.
The given heights are: 135, 150, 139, 128, 151, 132, 146, 149, 143, 141.
Comparing the values, the lowest height is 128 cm.
The height of the shortest girl is 128 cm.
(iii) What is the range of the data?
The range of the data is the difference between the highest and the lowest values.
Range = Highest height - Lowest height
Range = $151 - 128$
Range = $23$ cm
The range of the data is 23 cm.
(iv) What is the mean height of the girls?
The mean height is calculated by summing all the heights and dividing by the total number of girls.
Sum of heights = $135 + 150 + 139 + 128 + 151 + 132 + 146 + 149 + 143 + 141$
Sum of heights = $1414$ cm
Number of girls = 10
Mean height = $\frac{\text{Sum of heights}}{\text{Number of girls}}$
Mean height = $\frac{1414}{10}$
Mean height = $141.4$ cm
The mean height of the girls is 141.4 cm.
(v) How many girls have heights more than the mean height?
The mean height is 141.4 cm.
We need to count the number of girls whose height is greater than 141.4 cm from the given list:
135, 150, 139, 128, 151, 132, 146, 149, 143, 141
Heights greater than 141.4 cm are:
150 (> 141.4)
151 (> 141.4)
146 (> 141.4)
149 (> 141.4)
143 (> 141.4)
There are 5 girls with heights more than the mean height.
5 girls have heights more than the mean height.
Example 4 to 7 (Before Exercise 3.2)
Example 4. Find the mode of the given set of numbers:
| 1 | 1 | 2 | 4 | 3 | 2 | 1 | 2 | 2 | 4 |
Answer:
The given set of numbers is: 1, 1, 2, 4, 3, 2, 1, 2, 2, 4.
The mode of a set of data is the value that appears most frequently.
To find the mode, we can count the frequency of each unique number in the set:
- Number 1 appears 3 times.
- Number 2 appears 4 times.
- Number 3 appears 1 time.
- Number 4 appears 2 times.
The number that occurs most frequently in the given set is 2, as it appears 4 times, which is more than any other number.
Therefore, the mode of the given set of numbers is 2.
Example 5. Following are the margins of victory in the football matches of a league.
| 1 | 3 | 2 | 5 | 1 | 4 | 6 | 2 | 5 | 2 |
| 2 | 2 | 4 | 1 | 2 | 3 | 1 | 1 | 2 | 3 |
| 2 | 6 | 4 | 3 | 2 | 1 | 1 | 4 | 2 | 1 |
| 5 | 3 | 3 | 2 | 3 | 2 | 4 | 2 | 1 | 2 |
Find the mode of this data.
Answer:
The given margins of victory in the football matches are:
1, 3, 2, 5, 1, 4, 6, 2, 5, 2, 2, 2, 4, 1, 2, 3, 1, 1, 2, 3, 2, 6, 4, 3, 2, 1, 1, 4, 2, 1, 5, 3, 3, 2, 3, 2, 4, 2, 1, 2.
The mode of a set of data is the observation that occurs most frequently.
To find the mode, we can arrange the data or count the frequency of each observation. Let's make a frequency distribution table with tally marks.
| Margin of Victory | Tally Marks | Frequency |
| 1 | $\bcancel{||||}$$||||$ | 9 |
| 2 | $\bcancel{||||}$$ \bcancel{||||}$$||||$ | 14 |
| 3 | $\bcancel{||||}$$||$ | 7 |
| 4 | $\bcancel{||||}$ | 5 |
| 5 | $|||$ | 3 |
| 6 | $||$ | 2 |
From the frequency table, we can see that the margin of victory '2' occurs 14 times, which is the highest frequency.
Therefore, the mode of this data is 2.
Example 6. Find the mode of the numbers:
| 2 | 2 | 2 | 3 | 3 | 4 | 5 | 5 | 5 | 6 |
| 6 | 8 |
Answer:
The given set of numbers is: 2, 2, 2, 3, 3, 4, 5, 5, 5, 6, 6, 8.
The mode of a set of data is the value(s) that appear(s) most frequently.
To find the mode, we count the frequency of each number in the set:
- Number 2 appears 3 times.
- Number 3 appears 2 times.
- Number 4 appears 1 time.
- Number 5 appears 3 times.
- Number 6 appears 2 times.
- Number 8 appears 1 time.
Comparing the frequencies, we see that both the numbers 2 and 5 appear 3 times, which is the highest frequency among all the numbers in the set.
Since there are two values that appear with the highest frequency, this data set has two modes.
The modes of the given set of numbers are 2 and 5.
Example 7. Find the median of the data:
| 24 | 36 | 46 | 17 | 18 | 25 | 35 |
Answer:
The given data set is: 24, 36, 46, 17, 18, 25, 35.
The median is the middle value of a data set when it is arranged in ascending or descending order.
First, we need to arrange the data in ascending order:
17, 18, 24, 25, 35, 36, 46
The number of observations in the data set is 7.
Since the number of observations (n) is odd (n = 7), the median is the value at the $(\frac{n+1}{2})$-th position.
Median position = $\frac{7+1}{2} = \frac{8}{2} = 4$th position.
Looking at the ordered data (17, 18, 24, 25, 35, 36, 46), the value at the 4th position is 25.
Therefore, the median of the data is 25.
Exercise 3.2
Question 1. The scores in mathematics test (out of 25) of 15 students is as follows:
| 19 | 25 | 23 | 20 | 9 | 20 | 15 | 10 | 5 | 16 |
| 25 | 20 | 24 | 12 | 20 |
Find the mode and median of this data. Are they same?
Answer:
Given scores in mathematics test (out of 25) of 15 students are:
19, 25, 23, 20, 9, 20, 15, 10, 5, 16, 25, 20, 24, 12, 20.
The number of students (observations) is 15.
Find the Mode:
The mode is the value that appears most frequently in the data set.
Let's list the unique values and their frequencies:
- 5: 1 time
- 9: 1 time
- 10: 1 time
- 12: 1 time
- 15: 1 time
- 16: 1 time
- 19: 1 time
- 20: 4 times
- 23: 1 time
- 24: 1 time
- 25: 2 times
The score that appears most frequently is 20, which appears 4 times.
The mode of the data is 20.
Find the Median:
The median is the middle value of the data set when arranged in ascending or descending order.
Let's arrange the data in ascending order:
5, 9, 10, 12, 15, 16, 19, 20, 20, 20, 20, 23, 24, 25, 25
Since the number of observations ($n = 15$) is odd, the median is the value at the $(\frac{n+1}{2})$-th position.
Median position = $\frac{15+1}{2} = \frac{16}{2} = 8$th position.
In the ordered data set (5, 9, 10, 12, 15, 16, 19, 20, 20, 20, 20, 23, 24, 25, 25), the value at the 8th position is 20.
The median of the data is 20.
Are they same?
We found that the mode is 20 and the median is 20.
Yes, the mode and the median of this data are the same.
Question 2. The runs scored in a cricket match by 11 players is as follows:
| 6 | 15 | 120 | 50 | 100 | 80 | 10 | 15 | 8 | 10 |
| 15 |
Find the mean, mode and median of this data. Are the three same?
Answer:
The runs scored in a cricket match by 11 players are:
6, 15, 120, 50, 100, 80, 10, 15, 8, 10, 15.
The number of players (observations) is 11.
Find the Mean:
The mean is the sum of the runs divided by the number of players.
Sum of runs = $6 + 15 + 120 + 50 + 100 + 80 + 10 + 15 + 8 + 10 + 15$
Sum of runs = $429$
Number of players = 11
Mean runs = $\frac{\text{Sum of runs}}{\text{Number of players}}$
Mean runs = $\frac{429}{11}$
Mean runs = $39$
The mean run scored is 39.
Find the Mode:
The mode is the value that appears most frequently in the data set.
Let's list the unique values and their frequencies:
- 6: 1 time
- 8: 1 time
- 10: 2 times
- 15: 3 times
- 50: 1 time
- 80: 1 time
- 100: 1 time
- 120: 1 time
The score that appears most frequently is 15, which appears 3 times.
The mode of the data is 15.
Find the Median:
The median is the middle value of the data set when arranged in ascending or descending order.
Let's arrange the data in ascending order:
6, 8, 10, 10, 15, 15, 15, 50, 80, 100, 120
Since the number of observations ($n = 11$) is odd, the median is the value at the $(\frac{n+1}{2})$-th position.
Median position = $\frac{11+1}{2} = \frac{12}{2} = 6$th position.
In the ordered data set (6, 8, 10, 10, 15, 15, 15, 50, 80, 100, 120), the value at the 6th position is 15.
The median of the data is 15.
Are the three same?
We found that:
- Mean = 39
- Mode = 15
- Median = 15
The mean, mode, and median are not the same. The mode and median are equal (both 15), but the mean is different (39).
No, the mean, mode, and median of this data are not the same.
Question 3. The weights (in kg.) of 15 students of a class are:
| 38 | 42 | 35 | 37 | 45 | 50 | 32 | 43 | 43 | 40 |
| 36 | 38 | 43 | 38 | 47 |
(i) Find the mode and median of this data.
(ii) Is there more than one mode?
Answer:
Given the weights (in kg.) of 15 students of a class are:
38, 42, 35, 37, 45, 50, 32, 43, 43, 40, 36, 38, 43, 38, 47.
The number of students (observations) is 15.
(i) Find the mode and median of this data.
Mode:
The mode is the value(s) that appear(s) most frequently in the data set.
Let's count the frequency of each weight:
- 32: 1 time
- 35: 1 time
- 36: 1 time
- 37: 1 time
- 38: 3 times
- 40: 1 time
- 42: 1 time
- 43: 3 times
- 45: 1 time
- 47: 1 time
- 50: 1 time
The weights that appear most frequently are 38 and 43, both appearing 3 times.
The mode of the data is 38 and 43.
Median:
The median is the middle value of the data set when arranged in ascending or descending order.
Let's arrange the data in ascending order:
32, 35, 36, 37, 38, 38, 38, 40, 42, 43, 43, 43, 45, 47, 50
Since the number of observations ($n = 15$) is odd, the median is the value at the $(\frac{n+1}{2})$-th position.
Median position = $\frac{15+1}{2} = \frac{16}{2} = 8$th position.
In the ordered data set (32, 35, 36, 37, 38, 38, 38, 40, 42, 43, 43, 43, 45, 47, 50), the value at the 8th position is 40.
The median of the data is 40.
(ii) Is there more than one mode?
From the frequency count in part (i), we found that both 38 and 43 have the highest frequency (3 times).
Since two distinct values have the same highest frequency, there is more than one mode.
Yes, there is more than one mode. The modes are 38 and 43.
Question 4. Find the mode and median of the data:
| 13 | 16 | 12 | 14 | 19 | 12 | 14 | 13 | 14 |
Answer:
The given data set is: 13, 16, 12, 14, 19, 12, 14, 13, 14.
The number of observations is 9.
Find the Mode:
The mode is the value(s) that appear(s) most frequently in the data set.
Let's count the frequency of each number:
- 12: 2 times
- 13: 2 times
- 14: 3 times
- 16: 1 time
- 19: 1 time
The number that appears most frequently is 14, which appears 3 times.
The mode of the data is 14.
Find the Median:
The median is the middle value of the data set when arranged in ascending or descending order.
Let's arrange the data in ascending order:
12, 12, 13, 13, 14, 14, 14, 16, 19
Since the number of observations ($n = 9$) is odd, the median is the value at the $(\frac{n+1}{2})$-th position.
Median position = $\frac{9+1}{2} = \frac{10}{2} = 5$th position.
In the ordered data set (12, 12, 13, 13, 14, 14, 14, 16, 19), the value at the 5th position is 14.
The median of the data is 14.
Question 5. Tell whether the statement is true or false:
(i) The mode is always one of the numbers in a data.
(ii) The mean is one of the numbers in a data.
(iii) The median is always one of the numbers in a data.
(iv) The data 6, 4, 3, 8, 9, 12, 13, 9 has mean 9.
Answer:
(i) The mode is always one of the numbers in a data.
This statement is True.
The mode is defined as the value that appears most frequently in a data set. By its definition, it must be one of the values present in the data set.
(ii) The mean is one of the numbers in a data.
This statement is False.
The mean is the average of the data set, calculated by summing all values and dividing by the total number of values. The resulting mean may or may not be a value that is present in the original data set.
For example, the mean of the data set {1, 2, 3} is $\frac{1+2+3}{3} = 2$, which is in the data. However, the mean of the data set {1, 2, 4} is $\frac{1+2+4}{3} = \frac{7}{3} \approx 2.33$, which is not in the data set.
(iii) The median is always one of the numbers in a data.
This statement is False.
The median is the middle value of a data set when arranged in order. If the number of observations ($n$) is odd, the median is the single middle value and is always part of the data set. However, if the number of observations ($n$) is even, the median is the average of the two middle values. This average may or may not be one of the numbers in the data set.
For example, the median of the data set {1, 2, 3, 4} (arranged in order) is $\frac{2+3}{2} = 2.5$, which is not in the data set.
(iv) The data 6, 4, 3, 8, 9, 12, 13, 9 has mean 9.
This statement is False.
Let's calculate the mean of the given data: 6, 4, 3, 8, 9, 12, 13, 9.
Sum of data = $6 + 4 + 3 + 8 + 9 + 12 + 13 + 9 = 64$
Number of data points = 8
Mean = $\frac{\text{Sum of data}}{\text{Number of data points}} = \frac{64}{8} = 8$
The mean of the data is 8, not 9.
Example 8 to 10 (Before Exercise 3.3)
Example 8. Two hundred students of 6th and 7th classes were asked to name their favourite colour so as to decide upon what should be the colour of their school building. The results are shown in the following table. Represent the given data on a bar graph.
| Favourite Colour | Red | Green | Blue | Yellow | Orange |
|---|---|---|---|---|---|
| Number Of Students | 43 | 19 | 55 | 49 | 34 |
Answer the following questions with the help of the bar graph:
(i) Which is the most preferred colour and which is the least preferred?
(ii) How many colours are there in all? What are they?
Answer:
The given data shows the favourite colour of two hundred students from Class 6 and Class 7.
Representing the data on a bar graph:
To make a bar graph for this data, we will draw two lines, one going across (horizontal axis) and one going up (vertical axis).
On the horizontal axis, we will write the names of the colours: Red, Green, Blue, Yellow, and Orange. We can label this axis "Favourite Colour".
On the vertical axis, we will show the number of students. We need to choose a scale for this axis, like marking numbers in steps of 5 or 10 (0, 5, 10, 15, ...), up to a number slightly more than the highest number of students (which is 55). We can label this axis "Number of Students".
Then, for each colour, we draw a bar from the horizontal axis upwards, up to the height that shows the number of students who like that colour. The bars should be of the same width and have equal space between them.
The heights of the bars will be:
Red: 43
Green: 19
Blue: 55
Yellow: 49
Orange: 34
Here is what the bar graph would look like:
Now, let's answer the questions using the data (or the bar graph).
(i) Which is the most preferred colour and which is the least preferred?
The most preferred colour is the one with the highest bar (or the highest number of students).
From the table, the numbers are 43, 19, 55, 49, 34. The highest number is 55, which is for Blue.
The least preferred colour is the one with the lowest bar (or the lowest number of students).
The lowest number is 19, which is for Green.
So, the most preferred colour is Blue and the least preferred colour is Green.
(ii) How many colours are there in all? What are they?
The table lists the colours that were chosen by the students. Let's count them:
Red, Green, Blue, Yellow, Orange.
There are 5 colours in total.
They are: Red, Green, Blue, Yellow, and Orange.
Example 9. Following data gives total marks (out of 600) obtained by six children of a particular class. Represent the data on a bar graph.
| Students | Ajay | Bali | Dipti | Faiyaz | Geetika | Hari |
|---|---|---|---|---|---|---|
| Marks Obtained | 450 | 500 | 300 | 360 | 400 | 540 |
Answer:
The given data shows the total marks (out of 600) obtained by six students.
Representing the data on a bar graph:
To make a bar graph for this data, we will draw a horizontal axis and a vertical axis.
On the horizontal axis, we will write the names of the students: Ajay, Bali, Dipti, Faiyaz, Geetika, and Hari. We can label this axis "Students".
On the vertical axis, we will show the marks obtained by the students. We need to choose a suitable scale. Since the marks range from 300 to 540 (out of 600), we can choose a scale with intervals of 50 or 100, starting from 0. The vertical axis should go up to 600 or slightly more. We can label this axis "Marks Obtained".
Then, for each student, we draw a bar from the horizontal axis upwards, up to the height that shows their marks. The bars should be of the same width and have equal space between them.
The heights of the bars will be:
Ajay: 450
Bali: 500
Dipti: 300
Faiyaz: 360
Geetika: 400
Hari: 540
Here is what the bar graph would look like:
The bar graph helps us easily compare the marks of the different students.
Example 10. A mathematics teacher wants to see, whether the new technique of teaching she applied after quarterly test was effective or not. She takes the scores of the 5 weakest children in the quarterly test (out of 25) and in the half yearly test (out of 25):
| Students` | Ashish | Arun | Kavish | Maya | Rita |
|---|---|---|---|---|---|
| Quaterly | 10 | 15 | 12 | 20 | 9 |
| Half Yearly | 15 | 18 | 16 | 21 | 15 |
Answer:
The given data shows the scores of 5 students in two tests: Quarterly and Half Yearly. Both tests were out of 25 marks.
The teacher wants to compare the performance of each student in the two tests to see if the new teaching method helped.
To compare two sets of data for the same student, we can use a double bar graph.
To make a double bar graph, we will draw a horizontal axis and a vertical axis.
On the horizontal axis, we will write the names of the students: Ashish, Arun, Kavish, Maya, and Rita. We can label this axis "Students".
On the vertical axis, we will show the marks obtained. We need to choose a suitable scale for marks out of 25, for example, steps of 2 or 5 (0, 5, 10, 15, 20, 25). We can label this axis "Marks Obtained".
For each student, we will draw two bars side-by-side:
One bar will show the score in the Quarterly test, and the other bar will show the score in the Half Yearly test.
We should use different colours or patterns for the Quarterly bars and the Half Yearly bars, and explain what each colour/pattern means in a legend.
The heights of the bars for each student will be:
Ashish: Quarterly 10, Half Yearly 15
Arun: Quarterly 15, Half Yearly 18
Kavish: Quarterly 12, Half Yearly 16
Maya: Quarterly 20, Half Yearly 21
Rita: Quarterly 9, Half Yearly 15
There should be equal space between the pairs of bars for each student.
Here is what the double bar graph would look like:
By looking at the double bar graph, we can see how each student's marks changed from the Quarterly test to the Half Yearly test, which helps the teacher see if the new technique worked.
Exercise 3.3
Question 1. Use the bar graph (Fig 3.3) to answer the following questions.
Fig 3.3
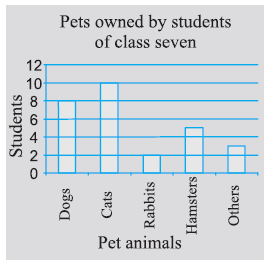
(a) Which is the most popular pet?
(b) How many students have dog as a pet?
Answer:
The answers are based on the interpretation of the bar graph shown in Fig 3.3.
(a) Which is the most popular pet?
To find the most popular pet, we look for the bar with the greatest height, as the height represents the number of students.
From the bar graph:
- Dogs: 8 students
- Cats: 10 students
- Rabbits: 2 students
- Hamsters: 5 students
- Others: 3 students
The bar for 'Cats' is the tallest, indicating that 10 students have cats as pets, which is the highest number.
Therefore, the most popular pet is Cat.
(b) How many students have dog as a pet?
To find the number of students who have a dog as a pet, we look at the height of the bar corresponding to 'Dogs'.
From the bar graph, the bar for 'Dogs' reaches the mark representing 8 on the vertical axis (Number of Students).
Therefore, 8 students have dog as a pet.
Question 2. Read the bar graph (Fig 3.4) which shows the number of books sold by a bookstore during five consecutive years and answer the following questions:
Fig 3.4

(i) About how many books were sold in 1989? 1990? 1992?
(ii) In which year were about 475 books sold? About 225 books sold?
(iii) In which years were fewer than 250 books sold?
(iv) Can you explain how you would estimate the number of books sold in 1989?
Answer:
We interpret the given bar graph (Fig 3.4) to answer the questions about the number of books sold by a bookstore.
The vertical axis represents the number of books sold. The scale shows that the space between major markings (like 0 and 100, 100 and 200) is divided into 10 smaller parts. This means each small part represents $\frac{100}{10} = 10$ books.
From the bar graph, we can read the number of books sold in each year:
1989: The bar reaches 7 small parts above 100. So, $100 + 7 \times 10 = 170$ books.
1990: The bar reaches 5 small parts above 400. So, $400 + 5 \times 10 = 450$ books.
1991: The bar reaches 2 small parts above 300. So, $300 + 2 \times 10 = 320$ books.
1992: The bar reaches 2 small parts above 200. So, $200 + 2 \times 10 = 220$ books.
1993: The bar reaches the 600 mark. So, 600 books.
(i) About how many books were sold in 1989? 1990? 1992?
In 1989: About 170 books were sold.
In 1990: About 450 books were sold.
In 1992: About 220 books were sold.
(ii) In which year were about 475 books sold? About 225 books sold?
We look for the year where the number of books sold is closest to 475 and 225.
For 475 books, the closest number sold is 450, which was in the year 1990.
For 225 books, the closest number sold is 220, which was in the year 1992.
About 475 books were sold in 1990.
About 225 books were sold in 1992.
(iii) In which years were fewer than 250 books sold?
We look at the number of books sold in each year and see which years have values less than 250.
1989: 170 (< 250)
1990: 450 (> 250)
1991: 320 (> 250)
1992: 220 (< 250)
1993: 600 (> 250)
Fewer than 250 books were sold in the years 1989 and 1992.
(iv) Can you explain how you would estimate the number of books sold in 1989?
To estimate the number of books sold in 1989 from the bar graph, we follow these steps:
1. Locate the bar representing the year 1989 on the horizontal axis.
2. Look at the height of the top of this bar.
3. Move horizontally from the top of the bar to the vertical axis (Number of Books Sold).
4. Observe the scale on the vertical axis. The space between 100 and 200 is divided into 10 equal parts, so each part represents 10 books.
5. The top of the bar for 1989 is above the 100 mark and aligns with the 7th small division above 100.
6. Therefore, the number of books sold is 100 plus the value of 7 small divisions, which is $100 + 7 \times 10 = 100 + 70 = 170$.
Thus, we estimate that 170 books were sold in 1989.
Question 3. Number of children in six different classes are given below. Represent the data on a bar graph.
| Class | Fifth | Sixth | Seventh | Eighth | Ninth | Tenth |
|---|---|---|---|---|---|---|
| Number Of Children | 135 | 120 | 95 | 100 | 90 | 80 |
(a) How would you choose a scale?
(b) Answer the following questions:
(i) Which class has the maximum number of children? And the minimum?
(ii) Find the ratio of students of class sixth to the students of class eight.
Answer:
The given data shows the number of children in six classes.
Representing the data on a bar graph:
We draw a bar graph with "Class" on the horizontal axis and "Number of Children" on the vertical axis.
(a) How would you choose a scale?
The number of children ranges from 80 to 135. A suitable scale for the vertical axis would be 1 unit representing 10 children. This way, we can easily show numbers like 80 (8 units), 90 (9 units), 100 (10 units), 120 (12 units), 135 (13.5 units). The axis should go up to at least 140.
Here is what the bar graph would look like:
(b) Answer the following questions:
(i) Which class has the maximum number of children? And the minimum?
Looking at the numbers: 135, 120, 95, 100, 90, 80.
The largest number is 135, which is for Class Fifth.
The smallest number is 80, which is for Class Tenth.
The class with the maximum number of children is Fifth.
The class with the minimum number of children is Tenth.
(ii) Find the ratio of students of class sixth to the students of class eight.
Number of students in Class Sixth = 120
Number of students in Class Eighth = 100
Ratio of Class Sixth to Class Eighth = $\frac{\text{Number of students in Class Sixth}}{\text{Number of students in Class Eighth}} = \frac{120}{100}$.
We simplify the fraction by dividing the top and bottom by a common number, like 20:
$\frac{\cancel{120}^{6}}{\cancel{100}_{5}} = \frac{6}{5}$.
The ratio is 6:5.
Question 4. The performance of a student in 1st Term and 2nd Term is given. Draw a double bar graph choosing appropriate scale and answer the following:
| Subject | English | Hindi | Maths | Science | S.Science |
|---|---|---|---|---|---|
| 1st Term (M.M 100) | 67 | 72 | 88 | 81 | 73 |
| 2nd Term (M.M 100) | 70 | 65 | 95 | 85 | 75 |
(i) In which subject, has the child improved his performance the most?
(ii) In which subject is the improvement the least?
(iii) Has the performance gone down in any subject?
Answer:
The given data shows a student's marks in two tests for five subjects.
We draw a double bar graph with "Subject" on the horizontal axis and "Marks Obtained" on the vertical axis.
We choose a scale for the vertical axis. Since marks are out of 100, we can use 1 unit to represent 10 marks, going from 0 up to 100.
For each subject, we draw two bars next to each other: one for the 1st Term marks and one for the 2nd Term marks. We use different colours and a key (legend) to show which bar is which term.
The bar heights are:
- English: 1st Term 67, 2nd Term 70
- Hindi: 1st Term 72, 2nd Term 65
- Maths: 1st Term 88, 2nd Term 95
- Science: 1st Term 81, 2nd Term 85
- S.Science: 1st Term 73, 2nd Term 75
The double bar graph would look like this:
To answer the questions, we look at the change in marks from the 1st Term to the 2nd Term (2nd Term marks - 1st Term marks).
- English: $70 - 67 = +3$
- Hindi: $65 - 72 = -7$
- Maths: $95 - 88 = +7$
- Science: $85 - 81 = +4$
- S.Science: $75 - 73 = +2$
Positive change means improvement, negative change means performance went down.
(i) In which subject, has the child improved his performance the most?
We look for the biggest positive change. The positive changes are +3, +7, +4, +2. The biggest positive change is +7.
The child improved the most in Maths.
(ii) In which subject is the improvement the least?
We look for the smallest positive change among the subjects that improved. The subjects with positive change are English (+3), Maths (+7), Science (+4), S.Science (+2). The smallest positive change is +2.
The improvement is the least in S.Science among the subjects that showed improvement.
(iii) Has the performance gone down in any subject?
We look for a negative change in marks.
The change in Hindi is -7, which is a negative number.
Yes, the performance has gone down in Hindi.
Question 5. Consider this data collected from a survey of a colony.
| Favourite Sport | Cricket | Basket Ball | Swimming | Hockey | Athletics |
|---|---|---|---|---|---|
| Watching | 1240 | 470 | 510 | 430 | 250 |
| Participating | 620 | 320 | 320 | 250 | 105 |
(i) Draw a double bar graph choosing an appropriate scale. What do you infer from the bar graph?
(ii) Which sport is most popular?
(iii) Which is more preferred, watching or participating in sports?
Answer:
The given data shows how many people in a colony like watching or participating in different sports.
(i) Draw a double bar graph choosing an appropriate scale. What do you infer from the bar graph?
We draw a double bar graph. We use a horizontal axis for "Favourite Sport" and a vertical axis for "Number of People".
We choose a scale for the vertical axis. Since the numbers go up to 1240, a good scale would be 1 unit representing 100 people. We mark the axis in steps like 0, 100, 200, ..., up to 1300.
For each sport, we draw two bars side-by-side: one for "Watching" and one for "Participating". We use different colours (e.g., blue for Watching, red for Participating) and a key.
The bar heights will be:
- Cricket: Watching 1240, Participating 620
- Basket Ball: Watching 470, Participating 320
- Swimming: Watching 510, Participating 320
- Hockey: Watching 430, Participating 250
- Athletics: Watching 250, Participating 105
The double bar graph would look like this:
Inference from the bar graph: We can see that for every sport, more people prefer watching it than participating in it. Cricket is the most popular sport overall, both for watching and participating.
(ii) Which sport is most popular?
The most popular sport is the one that the most people like, either watching or participating. We can find the total number of people for each sport by adding Watching and Participating numbers.
- Cricket: $1240 + 620 = 1860$
- Basket Ball: $470 + 320 = 790$
- Swimming: $510 + 320 = 830$
- Hockey: $430 + 250 = 680$
- Athletics: $250 + 105 = 355$
Cricket has the highest total (1860).
The most popular sport is Cricket.
(iii) Which is more preferred, watching or participating in sports?
We add up the total number of people who prefer watching across all sports, and the total number who prefer participating across all sports.
Total Watching = $1240 + 470 + 510 + 430 + 250 = 2900$
Total Participating = $620 + 320 + 320 + 250 + 105 = 1615$
Since $2900 > 1615$, watching is preferred by more people.
Watching sports is more preferred.
Question 6. Take the data giving the minimum and the maximum temperature of various cities given in the beginning of this Chapter (Table 3.1). Plot a double bar graph using the data and answer the following:
(i) Which city has the largest difference in the minimum and maximum temperature on the given date?
(ii) Which is the hottest city and which is the coldest city?
(iii) Name two cities where maximum temperature of one was less than the minimum temperature of the other.
(iv) Name the city which has the least difference between its minimum and the maximum temperature.
Answer:
To answer these questions, we need the data from Table 3.1. Let's assume the data is available and is as follows:
Ahmedabad: Min 29°C, Max 38°C
Amritsar: Min 26°C, Max 37°C
Bangalore: Min 21°C, Max 28°C
Chennai: Min 29°C, Max 36°C
Delhi: Min 28°C, Max 38°C
Jaipur: Min 29°C, Max 39°C
Jammu: Min 26°C, Max 41°C
Mumbai: Min 27°C, Max 32°C
Draw a double bar graph:
We draw a double bar graph with "City" on the horizontal axis and "Temperature (°C)" on the vertical axis. We choose a scale like 1 unit = 5°C, going from 0°C up to 45°C.
For each city, we draw two bars side-by-side: one for Minimum Temp and one for Maximum Temp, using different colours and a key.
The double bar graph would look like this:
Now, we answer the questions based on the data:
(i) Which city has the largest difference in the minimum and maximum temperature?
We calculate the difference (Max Temp - Min Temp) for each city:
- Ahmedabad: $38 - 29 = 9^\circ\text{C}$
- Amritsar: $37 - 26 = 11^\circ\text{C}$
- Bangalore: $28 - 21 = 7^\circ\text{C}$
- Chennai: $36 - 29 = 7^\circ\text{C}$
- Delhi: $38 - 28 = 10^\circ\text{C}$
- Jaipur: $39 - 29 = 10^\circ\text{C}$
- Jammu: $41 - 26 = 15^\circ\text{C}$
- Mumbai: $32 - 27 = 5^\circ\text{C}$
The largest difference is 15°C.
Jammu has the largest difference in temperature.
(ii) Which is the hottest city and which is the coldest city?
Hottest city is the one with the highest maximum temperature. The highest maximum temperature is 41°C (Jammu).
Coldest city is the one with the lowest minimum temperature. The lowest minimum temperature is 21°C (Bangalore).
The hottest city is Jammu.
The coldest city is Bangalore.
(iii) Name two cities where maximum temperature of one was less than the minimum temperature of the other.
We need to find City A and City B such that Max Temp of A < Min Temp of B.
Looking at the data, let's check Bangalore (Max 28°C). Are there any cities with Min Temp > 28°C?
Ahmedabad (Min 29°C), Chennai (Min 29°C), Delhi (Min 28°C), Jaipur (Min 29°C).
So, Bangalore's maximum temperature (28°C) is less than the minimum temperature of Ahmedabad (29°C), Chennai (29°C), and Jaipur (29°C).
Two such cities could be Bangalore (Max 28°C) and Ahmedabad (Min 29°C).
Or Bangalore (Max 28°C) and Chennai (Min 29°C).
Or Bangalore (Max 28°C) and Jaipur (Min 29°C).
(iv) Name the city which has the least difference between its minimum and the maximum temperature.
We look for the smallest difference calculated in part (i). The differences are 9, 11, 7, 7, 10, 10, 15, 5.
The smallest difference is 5°C, which is for Mumbai.
The city with the least difference is Mumbai.

